|
 |
| Korean J Ophthalmol > Volume 36(3); 2022 > Article |
|
Abstract
Purpose
Various types of trauma can cause retinal hemorrhages in children, including accidental and nonaccidental head trauma. We used animal eyes and a finite element model of the eye to examine stress patterns produced during purely linear and angular accelerations, along with stresses attained during simulated repetitive shaking of an infant.
Methods
Using sheep and primate eyes, sclerotomy windows were created by removing the sclera, choroid, and retinal pigment epithelium to expose the retina. A nanofiber square was glued to a 5 mm2 area of retina. The square was pulled and separated from vitreous while force was measured. A finite element model of the pediatric eye was used to computationally measure tension stresses during shaking.
Results
In both sheep and primate eyes, tension stress required for separation of retina from vitreous range from 1 to 5 kPa. Tension stress generated at the vitreoretinal interface predicted by the computer simulation ranged from 3 to 16 kPa during a cycle of shaking. Linear acceleration generated lower tension stress than angular acceleration. Angular acceleration generated maximal tension stress along the retinal vasculature. Linear acceleration produced more diffuse force distribution centered at the poster pole.
Conclusions
The finite element model predicted that tension stress attained at the retina during forcible shaking of an eye can exceed the minimum threshold needed to produce vitreoretinal separation as measured in animal eyes. Furthermore, the results show that movements that involve significant angular acceleration produce strong stresses localized along the vasculature, whereas linear acceleration produces weaker, more diffuse stress centered towards the posterior pole of the eye.
Retinal hemorrhages (RH) can be caused by many different forms of trauma such as automobile collisions, sports-related injuries, and other mechanisms of blunt trauma to the eye. Among infants, the most common cause for RH is abusive head trauma (AHT), in which hemorrhages have been observed in approximately 85% of child victims of AHT [1-3]. AHT is part of a clinical constellation, previously known as shaken baby syndrome, and is a form of inflicted head trauma in infants usually less than 3 years of age. As the leading cause of infant mortality and morbidity from injurious etiology, prevalence in the United States has been estimated to occur in 30 out of 100,000 children under the age of 1 [4-7]. It can result in characteristic injury to the central nervous system, skeleton, and eyes, particularly when the victim is subjected to repetitive acceleration-deceleration, with or without blunt head trauma. In some cases, RH may be the principal or only diagnostic feature suggesting the possibility of AHT.
Since the first description of RH in whiplash syndrome by Caffey [8] in 1946, model studies have shown that translational oscillatory movements in conjunction with a centrifugal force from multiplanar displacements could produce RH in infants with no other history of direct contact trauma [8-10]. Many of these cases display RH with multilayered involvement extending out to the ora serrata, with or without macular retinoschisis. However, other forms of trauma, including vaginal delivery, can also induce RH in infants. In the present study, we measured conditions that can mimic clinical features of child abuse which contribute to ongoing controversies in this field with many discrediting the existence of AHT associated with RH and brain injury. When comparing oscillatory motion with a single traumatic impact, there are qualitative and quantitative differences in clinical presentation. Therefore, we hypothesized that the traction stresses produced in the retina may be particularly effective at producing the multilayered and multifocal patterns of RH that are typically found in AHT.
In this report, we developed a method for directly measuring the traction force at the vitreoretinal interface using eyes from monkeys and young sheep. The objective of the animal portion of the study was to determine the force needed to separate the retina from the vitreous in an ex vivo eye. Sheep eyes were chosen for their similarity in size and tissue characteristics to the retina and vitreous of juvenile human eyes. Monkey eyes were also used for their similarity to human eyes in regards to ocular development and emmetropization [11-15]. Subsequently, we utilized a finite element (FE) analysis of the eye that could be exposed to virtual forces. We had previously used this model to measure shear stresses, in addition to tractional and compressive forces, experienced in different parts of the eye, employing parameters measured in a biomimetic infant dummy doll during shaking by a human adult [16]. In the present study, we used the FE model to evaluate traction stress. Shaking motions involve a continually varying combination of rotational and linear acceleration; to discern the contribution of these two forces, we also examined the stress patterns produced during pure linear and pure rotational acceleration. We compared the stress values predicted by the FE model to traction stress measured directly in monkey and sheep eyes.
From this study, our findings indicate that the stress levels experienced during rotational movements such as those experienced during shaking are much more likely to cause separation between the vitreous and retina than purely linear movements and generate multifocal patterns of RH that are typical of AHT. These results provide guidance about the likelihood and patterns of vitreoretinal separation under different conditions. This knowledge can be helpful in developing future guidelines and educational material about the risks and hazards associated with other activities, such as sports-related injuries and automobile accidents.
All animals were maintained at the Department of Comparative Medicine at the University of Nebraska Medical Center in accordance with the rules and regulations of the International Care and Use Committee and according to the guidelines of the Committee on the Care and Use of Laboratory Animal Resources (No. 15-09-023-ABL2), National Research Council and the Department of Health and Human Services outlined in “Guide for the Care and Use of Laboratory Animals.” All protocols and procedures were performed under approval of the Institutional Animal Care and Use Committee of University of Nebraska Medical Center according to the National Institute of Health guidelines.
The methods and parameters used in the FE model of the human eye were described by our previous study [16]. Briefly, we previously developed a streamlined model that retained the sclera, vitreous, and retina but excluded the anterior segment. The sclera and retina had a hollow spherical shape, with an outer diameter of 26 mm and 24.5 mm, a thickness of 0.8 mm and 0.25 mm. The vitreous was considered as a filled spherical shape with a diameter of 24 mm (Fig. 1A) [16]. Three thin layers were incorporated into the retina to simulate preretinal, intraretinal, and subretinal layers. A tie constraint ties the outer surface of the retina and the inner surface of the sclera together so that there is no relative motion between them. Vitreoretinal attachment points were incorporated along retinal vessels, the posterior pole, and the vitreous base of the eye globe (Fig. 1B) [16].
In addition, kinematic contact method by tangential behavior and hard contact as a pressure-overclosure in the FE software dedicated between retina and vitreous. The mesh density analyses under various element numbers have been performed. Elements type for all three components considered as a C3D8R an 8-node Hex linear brick, reduce integration and hourglass control. The material properties and number of elements for each component are listed in Table 1. The nonlinear stress-strain relationship of the sclera is shown in Fig. 2. As described earlier, we subjected this FE model to a shaking frequency of 2.2 Hz (12.6 rad/sec) for one shaking cycle [16]. When studying purely linear or rotational acceleration, we used a force of 3.7g. This yielded a linear acceleration of 36.4 m/sec2 and an angular acceleration of 182 rad/sec2 when moved through a radius of 20 cm. The data were analyzed on a continuous basis in a dynamic fashion to calculate the force and pressure applied to the elements and the nodes at any given point. Following simulation, the tensile stresses along the radial direction were extracted and compared with the experimental data. Further details of the FE model and its subsequent findings can be found in our preceding study [16].
To complement our FE model, an ex vivo model was employed to further characterize purely linear and angular acceleration forces on native animal tissue. Eyeballs (n = 7) were harvested from sheep 6 to 9 months of age (Sierra Medical, Whittier, CA, USA) and were immediately placed in 4°C and shipped within 12 hours of recovery. Eyeballs were experimentally utilized within 24 hours upon receipt. Orbital fat, fascia, and extraocular muscles were carefully dissected away, and the optic nerve left intact. An 8 × 8 mm sclerotomy was performed 8 mm lateral to the optic nerve for the first group of three eyeballs and 20 mm lateral for the second group of four eyeballs to the forces required for vitreoretinal separation in different regions of the retina. Then, along with the sclera, the choroid and the retinal pigment epithelium were carefully separated from the retina by an experienced pediatric ophthalmologist using a microscope. The underlying retina was inscribed using a 15°, 1.5 mm depth microsharp blade, leaving a 5 × 5 mm area of retina held in place by the underlying vitreous attachments, which were undisturbed by this isolation of the small square of retina (Fig. 3A, 3B, 4A-4C). A 5 × 5 mm square pad of rigid polytetrafluoroethylene (PTFE) material was glued onto the scored retinas with polyurethane adhesives (Fig. 3C). Various adhesives were tested to maximize the adhesion of the retina to the PTFE. Cyanoacrylate failed on the moist, smooth surface of the retina, and its exothermic reaction with the surface of the retina distorted the anatomy. Epoxy resins were difficult to apply in a small area and in a moist environment, adhesion was not adequate. Nonheat-generating polyurethane was the best agent to adhere the retina to the PTFE.
A three dimensional-printed suction cup was glued onto the de-epithelialized cornea (Fig. 3D). A load cell, a transducer that converts force into electrical output, of the CellScale BioTester (Waterloo, ON, Canada) and associated actuators were attached to both the suction cup and PTFE square, by way of a 5.0 Mersilene suture through the center of the PTFE square (Fig. 3D). Actuators were pulled in opposite 180° directions at a constant velocity (1 mm/sec), y-displacement (0°), and temperature (37°C) until a complete tear was achieved (Fig. 3E, 4D). The length of the suture was long enough to maintain the force in constant tension in line with the actuator movement. For four initial experiments, the retina and glued PTFE square were placed perpendicular to the actuators. The primary force of the deformation of the vitreous and its separation from retina was mostly tensile or normal stress, with the amount of shearing stress being negligible. The procedure was repeated three times with the glued PTFE square at a tangential angle with respect to the actuator. In these angled experiments, the force of deformation of the vitreous and its separation from the retina was due to a combination of normal and shear stress components. The forces at which a vitreoretinal tear began were measured in millinewtons (mN), then converted to units of stress (kPa) by dividing by the area of the PTFE material.
Two female Rhesus macaques were euthanized between ages 5 and 6 years old via ketamine overdose and saline perfusion (10 L). Adult female Indian-origin Rhesus macaques (Macaca mulatta) were utilized in this study. No obvious abnormalities were noted in the monkeys during necropsy and eyeballs, amongst other vital organ tissues, were harvested and used experimentally within 12 hours (Fig. 5A). The above procedure performed on sheep eyeballs was repeated with the monkey eyeballs (Fig. 5B). However, given the more fragile nature of monkey eye tissue, the rigid PTFE material was replaced with a softer and thinner nanofiber material square, with the suture passed through the material, then glued with polyurethane directly onto exposed retina.
We performed a sclerotomy at either 0° or 45° with respect to the horizontal axis, from the optic nerve to the center of the cornea using seven sheep eyes and two monkey eyes. As aforementioned in the Materials and Methods, we then measured the forces required to separate the 5 × 5 mm section of retina from the vitreous. The separation angle was set at 0° for the first four sheep eyes, yielding an average traction stress of 2.72 ± 1.65 kPa (0.95 standard error of the mean [SEM]). The separation angle was then set at 45° for the next three sheep eyes. The steeper angle involves both traction and shear stress and required a higher overall stress for separation of 4.25 ± 1.19 kPa (0.59 SEM). The peak stress attained in both conditions was 5.13 kPa (Table 2). Due to the scarcity of freshly necropsied monkey tissue, only two monkey eyeballs were tested, both at 0°. The average traction stress in the two eyeballs was 1.41 kPa, with the greatest stress reaching 1.5 kPa.
Using FE analysis of the human eye, the von Mises stress values were determined for different regions of the retina when shaking a baby. We utilized values measured from a biometric infant model to simulate shaking. The pattern of movements during a single cycle of shaking at 2.2 Hz is shown in Fig. 6A. The linear and angular components of acceleration varied throughout the cycle, as shown in Fig. 6B and 6C, respectively. Linear acceleration ranged from −118 m/sec2 to +89 m/sec2, with an average of 32.4 m/sec2. Angular acceleration revealed a brief bimodal peak when the direction of motion was reversed, with a rapid drop to −2382 rad/sec2 that rapidly reversed +3135 rad/sec2. These data are resultant from our precedent work establishing the FE model [16].
As found for shear stress in our earlier model, we determined that the greatest amount of traction stress experienced throughout the retina was concentrated along the vasculature, especially at vessel bifurcations [16]. Fig. 7A shows the pattern of stress values at the final time point of the cycle (0.44 second). Stress ranged from 3 kPa in non-vascular regions of the retina to as much as 16 kPa (red points in Fig. 7A), exceeding the traction stress needed for vitreoretinal separation. Fig. 7B shows the changes at a single point in the retina (arrow in Fig. 7A) in regard to dynamic traction stress during the cycle. The peak values of tensile stress in each layer are also shown in Fig. 7C: the preretinal layer experienced the highest tensile stress of 15.7 kPa, the intraretinal layer attained 11.8 kPa, and the subretinal layer with 8.0 kPa. The differences in tensile stress are statistically significant between the subretinal and preretinal layers (p = 0.01), with means of 5.04 and 3.92 kPa, respectively; as well as the intraretinal and preretinal layers (p = 0.05) with means of 4.40 and 3.92 kPa, respectively.
The FE model was also used in this study to analyze the forces experienced during purely linear and purely rotational acceleration. For linear acceleration, we chose a value of 3.7g (36.4 m/sec2), congruous to the average linear acceleration experienced during a cycle of shaking. This is also in line with the averages of linear acceleration experienced by young recreational players while heading a soccer ball [17]. During a 0.1 second period of pure linear acceleration, the FE model revealed a diffuse distribution of stress across the retina, centered toward the posterior pole, with some values less than 0.37 kPa (Fig. 8A-8D). Fig. 8 further illustrates stress measurements at a given point of the retina (arrows, in Fig. 8A and 8B) remaining relatively constant throughout one cycle of shaking.
While activities such as heading a soccer ball produces little rotational force, shaking a baby involves significant angular components [17]. As shown in Fig. 8B, the amount and patterns of traction stress generated during pure angular acceleration of 3.7g differed from those of linear acceleration, with tenfold higher peak stress values and a more focal pattern that respected the retinal vasculature. Fig. 8D shows time-dependent changes during a 0.1 second trial of angular acceleration measured at a single point in the eye. The tension stress rose continuously during the trial, reaching 3.7 kPa, exceeding the tension stress required for vitreoretinal separation. The FE model also revealed that stress values could differ quite substantially at neighboring points. As seen in Fig. 8B, there are a number of areas in the retina where peak positive (red elements) and negative (blue elements) stress values are present at points very close to one another. These large stress gradients could increase the likelihood of vitreoretinal separation and hemorrhage.
These results infer that the stress generated during shaking exceed the traction stress for vitreoretinal attachment. It is reasonable to infer this stress could exceed the threshold of vitreoretinal attachment to induce tearing along the retinal vessels, causing hemorrhages throughout the retina. Purely linear acceleration produced tenfold weaker tension stress than angular acceleration with stress focused diffusely at the posterior pole of the eye. Purely angular acceleration generated higher stress values concentrated along the blood vessels, closely mirroring the patterns observed during shaking.
Our numerical conclusions combined empirical measurements of the forces required for vitreoretinal detachment with a FE model of the pediatric eye. The pattern and level of stresses experienced during purely linear acceleration differed considerably from that experienced during angular acceleration. Linear acceleration involved much lower stresses that were distributed diffusely across the posterior pole whereas angular acceleration generated larger tension stress concentrated along the retinal vasculature. In addition, angular acceleration generated large stress gradients with regions of large positive stress immediately adjacent to large negative stress. These results suggest that movements involving angular acceleration are much more likely to produce vitreoretinal detachment and RH than movements involving only linear acceleration.
To measure vitreoretinal detachment forces, we used two animal models in which the vitreoretinal interface is similar to humans. The obstacle of experimenting on human tissue for this experiment warranted surrogate animal eyeballs that closely resembled properties of the infant eye [13,18]. Eyes from young sheep were chosen due to their coronal and sagittal dimensions, as well as their hyaluronic acid and collagenous vitreous compositions, which are similar to the infantile human eyeball [11-14,19]. These sheep eyes were harvested from animals approximately 6 to 9 months old, which is equivalent to around 2 to 4 years of human age. Rhesus macaque eyes were chosen as the developmental processes during ocular maturation parallels human eye development. Particular similarities include retinal vasculature conformations, presence of a true macula, cellular distributions, and evidence of a dimensionally consistent perifoveal vascular ring [15,20]. Monkey eyes were harvested from animals approximately 5 to 6 years old, equivalent to around 18 to 19 years of human age. Although our monkeys were of adolescent age, studies show that the stiffness of the macaque sclera, while it does advance with age, is not significantly greater in infants compared to adolescent monkey [21-23]. An important feature of the human eye, shared only by primates, is the central visual pathway starting at the macula—an area dominated by cone photoreceptor cells. Primates are an invaluable model for exploring retinal anatomy and physiology as humans and macaques share susceptibility genes for retinal pathology in addition to providing reasonable inferences in terms of the biomechanics of the retina.
The results of the FE model suggest that different types of movement generate different stress patterns and so would be expected to produce different patterns of trauma in the eye. For example, properly heading a soccer ball produces almost purely linear acceleration but head-to-head collisions in soccer, football, rugby, and other sports can produce significant levels of both angular and linear acceleration [17,24]. We show a distinct difference in the amount and pattern of stresses generated during angular and linear acceleration, with much larger stresses attained during purely angular acceleration. In addition, the patterns obtained during purely angular acceleration revealed focal points along the vascular plexus whereas linear acceleration generated a more diffuse pattern radiating from the pole.
RH in infants subjected to abuse manifest multiple sub-types of retinal hemorrhages [25,26]. In comparison to a single blunt traumatic event, one forceful impact is unlikely to produce numerous RH throughout the panorama of the retina without significant external forces that would be obvious based on history. Infants delivered vaginally without complication may present with RH in up to 50% of the cases; however, our results suggest that a translational force, as seen in a unidirectional vaginal birth (without rotational and centrifugal force), produces a more diffuse pattern of RH concentrated at the poster pole, consistent with clinical observations [27]. When specifically considering RH with potential abuse etiology, extensive and careful medical and social history, and circumstances surrounding the events of the trauma are also essential.
Using our FE model to simulate shaking at 2.2 Hz, tension stress values were greatest along the vessels and vessel bifurcations [16]. This pattern is consistent with the large component of angular acceleration experienced during shaking. Tension stress values along the vasculature exceeded 10 kPa, well above the thresholds for vitreoretinal separation in both monkey and sheep eyes of 1.4 and 2.7 kPa, respectively. These results show that vigorous shaking can easily produce enough stress to the retina to separate the retina from vitreous. At frequencies of 2.2 Hz, the head of the infant travels a large distance resulting in increased traction and shear stress at the vitreoretinal interface. Although the range of motion can be more limited at higher frequencies, these higher frequencies are not realistically achievable [28]. Thus, given the stresses measured on the FE eye postshaking, corroborated by ex vivo eyeball manipulation experiments in conjunction with physical human limitations of accelerating the infant to maximum centrifugal forces, we can reasonably hypothesize that shaking an infant at a lower frequency is sufficient to produce AHT induced RH due to unique anatomical features of the infant musculoskeletal system.
Based on our two models, the computational data shows that shaking an infant at 2.2 cycles/sec frequency can produce stress levels that far exceed the minimum threshold for producing a vitreoretinal tear which may result in RH and other more severe potential outcomes including retinoschisis, retinal tear, and detachment, depending on the force generated. In our studies, external tensile force at two separate points on the retina, one just lateral to the optic nerve and the other 20 mm lateral to the nerve, show negligible differences in measured stress on the vitreous and retina. Future studies with animal eyeball studies will measure vitreoretinal stress due to differing angles of tangential force with respect to the horizontal to explore the shearing forces seen in all directions with AHT shaking. In addition, studies with ocular tissue that most closely aligns with neonatal and infantile ocular tissue would be ideal. With computed stress values climbing to 10 kPa in the FE model at areas of stronger vitreoretinal adhesions throughout the retina, we deduce the size, quantity, and location of RH found in AHT may correlate with the force generated during shaking. In conjunction with future animal model studies, future studies with the FE model can be modified to apply different parameters and forces induced in other types of traumas, specifically sports-related or secondary to automobile accidents.
Defining and characterizing AHT ebbs and flows with diagnostic criteria and legal protocols; even the disease entity name itself is in constant flux. What is under consensus is that a diagnosis of AHT requires significant interprofessional effort including extensive radiological and laboratory investigations and is mutually inclusive of clinical, legal, and social implications. With a large proportion of cases proceeding to severe morbidity and mortality, identifying clinical signs of abuse is critical. Ocular manifestations may be the only sign or clue that the child had undergone traumatic head injury and correlating the findings clinically should be a rigorous process. False negative diagnoses, placing the child back with the perpetrator, can often eventually lead to fatality. As a diagnosis of exclusion, similar differential diagnoses must be scrupulously ruled out to ensure implications of abuse are not introduced in cases without malicious intent [29,30]. These false positive diagnoses can also result in irreparable damage to the family dynamics and can have severe negative social impact.
In conclusion, ophthalmologists are often one of the first-line providers in intercepting potential cases of child abuse. By identifying cases with the unique characteristics of RH from AHT, the child abuse team is better equipped to make the most accurate diagnosis [4,25,31]. The current study focuses on understanding the forces generated to cause vitreoretinal separation, in hopes to educate the public and other medical specialists of the significant risk and clinical sequelae associated with shaking an infant. We demonstrated that repetitive acceleration-deceleration with compressive and tractional forces, stress accumulations due to repetition, and rotational-shearing force of the vitreoretinal interface play concerted roles in the development of retinal hemorrhagic sequelae following AHT [32]. Collaborative efforts to work together with pathologists, neurologists, pediatricians, and radiologists, will provide continued education about the dangers of this condition and to reduce alarmingly high case reports of AHT throughout the nation.
Acknowledgements
We thank Dr. Siddappa Byrareddy for the invaluable contribution of monkey tissue; Dr. Jesse Cox for his histopathological expertise; Dr. Alexey Kaminskiy for his generous lease of laboratory equipment; and Dr. Paul Deegan for his significant contribution of engineering logistics and know-how.
References
1. Gabaeff SC. Challenging the pathophysiologic connection between subdural hematoma, retinal hemorrhage and shaken baby syndrome. West J Emerg Med 2011;12:144-58.


2. Kivlin JD, Simons KB, Lazoritz S, Ruttum MS. Shaken baby syndrome. Ophthalmology 2000;107:1246-54.


4. Hedlund GL. Subdural hemorrhage in abusive head trauma: imaging challenges and controversies. J Am Osteopath Coll Radiol 2012;1:23-30.
5. Binenbaum G, Mirza-George N, Christian CW, Forbes BJ. Odds of abuse associated with retinal hemorrhages in children suspected of child abuse. J AAPOS 2009;13:268-72.



6. Schroeder L. Hot spots: pinpointing shaken baby syndrome cases [Internet] Evanston: Medill Justice Project; 2013 [cited 2018 Jan 16]. Available from: http://www.medilljustice-project.org/2013/12/10/hot-spots/
.
7. Keenan HT, Runyan DK, Marshall SW, et al. A population-based comparison of clinical and outcome characteristics of young children with serious inflicted and noninflicted traumatic brain injury. Pediatrics 2004;114:633-9.



8. Caffey J. The whiplash shaken infant syndrome: manual shaking by the extremities with whiplash-induced intracranial and intraocular bleedings, linked with residual permanent brain damage and mental retardation. Pediatrics 1974;54:396-403.


9. Yamazaki J, Yoshida M, Mizunuma H. Experimental analyses of the retinal and subretinal haemorrhages accompanied by shaken baby syndrome/abusive head trauma using a dummy doll. Injury 2014;45:1196-206.


10. Bonfiglio A, Lagazzo A, Repetto R, Stocchino A. An experimental model of vitreous motion induced by eye rotations. Eye Vis (Lond) 2015;2:10.



11. Prince JH, Diesem CD, Eglitis I, Ruskell GL. Anatomy and histology of the eye and orbit in domestic animals. Springfield: Charles C. Thomas; 1960.
12. Balazs EA, Denlinger JL. Aging changes in the vitreous. In: Sekuler R, Kline D, Dismukes K, Aging and human visual function. 2. New York: Alan R Liss; 1982. p. 45-57.
13. Colter J, Williams A, Moran P, Coats B. Age-related changes in dynamic moduli of ovine vitreous. J Mech Behav Biomed Mater 2015;41:315-24.


14. Nickerson CS, Park J, Kornfield JA, Karageozian H. Rheological properties of the vitreous and the role of hyaluronic acid. J Biomech 2008;41:1840-6.


15. Qiao-Grider Y, Hung LF, Kee CS, et al. Normal ocular development in young rhesus monkeys (Macaca mulatta). Vision Res 2007;47:1424-44.



16. Suh DW, Song HH, Mozafari H, Thoreson WB. Determining the tractional forces on vitreoretinal interface using a computer simulation model in abusive head trauma. Am J Ophthalmol 2021;223:396-404.


17. Reed WF, Feldman KW, Weiss AH, Tencer AF. Does soccer ball heading cause retinal bleeding? Arch Pediatr Adolesc Med 2002;156:337-40.


18. Coats B, Binenbaum G, Smith C, et al. Cyclic head rotations produce modest brain injury in infant piglets. J Neurotrauma 2017;34:235-47.



19. Saffioti JM, Coats B. Age dependent and anisotropic material properties of immature porcine sclera. In: Proceedings of the American Society of Mechanical Engineers (ASME) 2013 Summer Bioengineering Conference; 2013 Jun 26-29; Sunriver, USA. New York: AMSE; 2014.

20. Kong X, Wang K, Sun X, Witt RE. Comparative study of the retinal vessel anatomy of rhesus monkeys and humans. Clin Exp Ophthalmol 2010;38:629-34.


21. Yiu G, Wang Z, Munevar C, et al. Comparison of chorioretinal layers in rhesus macaques using spectral-domain optical coherence tomography and high-resolution histological sections. Exp Eye Res 2018;168:69-76.



22. Girard MJ, Suh JK, Bottlang M, et al. Biomechanical changes in the sclera of monkey eyes exposed to chronic IOP elevations. Invest Ophthalmol Vis Sci 2011;52:5656-69.



23. Girard MJ, Suh JK, Bottlang M, et al. Scleral biomechanics in the aging monkey eye. Invest Ophthalmol Vis Sci 2009;50:5226-37.



24. O’Connor KL, Rowson S, Duma SM, Broglio SP. Head-impact-measurement devices: a systematic review. J Athl Train 2017;52:206-27.



25. Bhardwaj G, Jacobs MB, Martin FJ, et al. Photographic assessment of retinal hemorrhages in infant head injury: the Childhood Hemorrhagic Retinopathy Study. J AAPOS 2017;21:28-33.


26. Yusuf IH, Barnes JK, Fung TH, et al. Non-contact ultra-widefield retinal imaging of infants with suspected abusive head trauma. Eye (Lond) 2017;31:353-63.



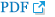
27. Kim SY, Morgan LA, Baldwin AJ, Suh DW. Comparison of the characteristics of retinal hemorrhages in abusive head trauma versus normal vaginal delivery. J AAPOS 2018;22:139-44.


28. Rossi T, Boccassini B, Esposito L, et al. The pathogenesis of retinal damage in blunt eye trauma: finite element modeling. Invest Ophthalmol Vis Sci 2011;52:3994-4002.


29. Jenny CA, Bertocci G, Fukuda T, et al. Biomechanical response of the infant head to shaking: an experimental investigation. J Neurotrauma 2017;34:1579-88.


30. Guthkelch AN. Infantile subdural haematoma and its relationship to whiplash injuries. Br Med J 1971;2:430-1.



Fig. 1
Human eyeball finite element model. (A) Eyeball components including vitreous, Retina and Sclera. (B) Retinal vessel attachment to the vitreous shown in the finite element model and three thin layers of the retina to represent preretinal, intraretinal, and subretinal layers. Adapted from Suh et al. [16] with permission from Elsevier.

Fig. 3
Sheep eyeball sclerotomy and biaxial planar force and displacement measurement. (A) Eyeball cleared of muscles, fat, and fascia with 8 × 8 mm square of sclera removed. (B) Sclera and choroid removed exposing retina still attached to vitreous. (C) Polytetrafluoroethylene square glued onto retina. (D) Eyeball secured to biaxial materials machine via load cells. (E) Retina with attached polytetrafluoroethylene square being pulled away from rest of eyeball by biaxial materials machine.

Fig. 4
Detailed view of sclerotomy. (A) Creating an 8 × 8 mm sclerotomy. (B) Demonstration by pediatric ophthalmologist. The pediatric ophthalmologist provided informed consent for publication of the image. (C) Scored retina throughout entire sclerotomy perimeter. (D) A retina square removed after being pulled by load cell of biaxial materials machine.

Fig. 5
Monkey eyeballs. (A) Two monkey eyeballs. (B) Monkey eyeball attached to load cells, to be pulled.
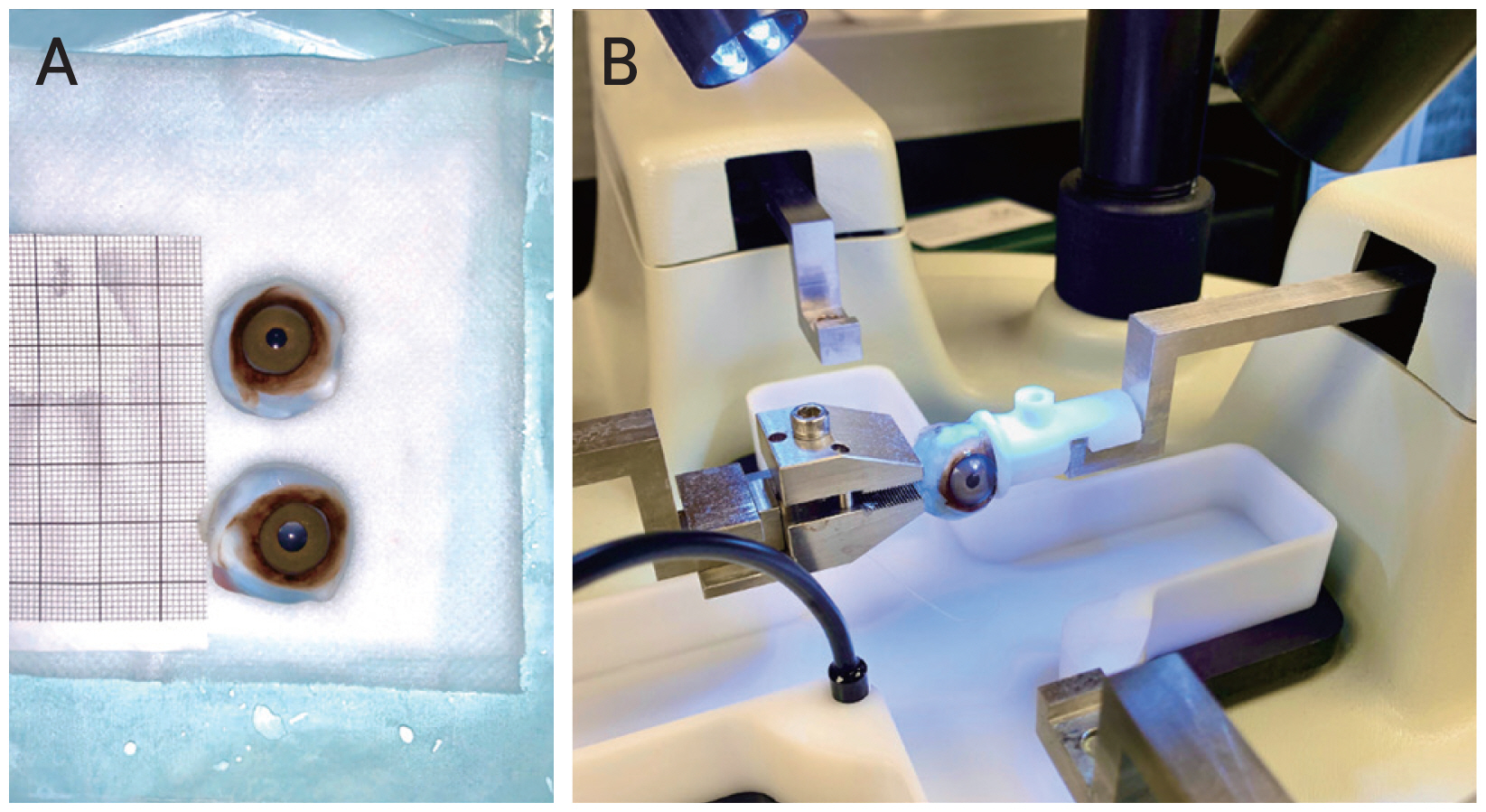
Fig. 6
Movement pattern and mechanics of finite element eye in one cycle of shaking. (A) Motion of the eyeball. (B) Linear acceleration. (C) Angular acceleration.
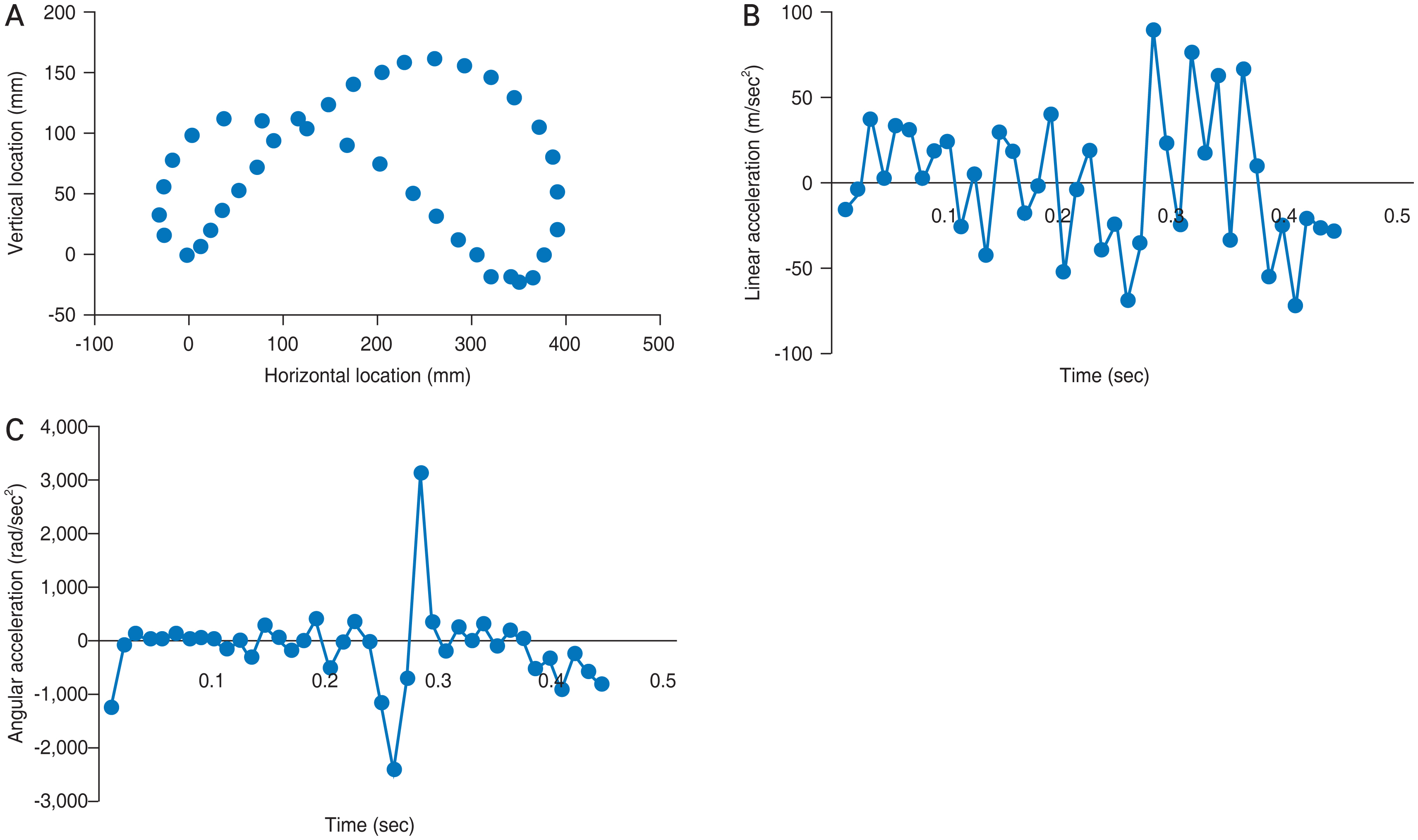
Fig. 7
Stress patterns of the finite element eye in one cycle of shaking. (A) Stress distribution in the retinal layer at the end of one shaking cycle (0.44 second). (B) History of tensile stress at a representative point. (C) The peak value of tensile stress in three layers.
Fig. 8
Tensile stress in retinal layer for (A) linear acceleration and (B) angular acceleration at 0.1 second. (C) The retinal vasculature. (D) Comparison between angular acceleration and angular acceleration.

Table 1
The number of elements, material model, density, and material parameters of the finite element model
| Model component | Material model | No. of elements | Density (kg/m3) | Material parameters |
|---|---|---|---|---|
| Sclera | Polynomial hyperelastic | 28,032 | 1,243 | Uniaxial test data (Fig. 2) |
| Retina | Elastic | 17,856 | 1,000 | E = 20 kPa, v = 0.49 |
| Vitreous | Viscoelastic | 103,968 | 1,009 | E = 43 kPa, v = 0.49, g-iProny* = 0.97, k-iProny* = 0, tau-iProny* = 0.07 |
- TOOLS




 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print